このページは約 13 分で読めます。有意義なページになっていますので、最後までご覧ください。
目次
中学2年生の数学で多くの生徒がつまずくのが「平行四辺形の証明」です。
「証明問題が苦手」、「何を書けばいいのかわからない」、「そもそも何をすればいいのかわからない」と悩んでいる生徒も少なくありません。
平行四辺形の証明は、図形の性質を正しく理解し、論理的に説明する力が求められるため、多くの中学生が苦手意識を抱えています。
しかし、平行四辺形の証明は、基本的なパターンと考え方を身につけることで、確実に解けるようになりますので、コツさえ掴めば「得意単元」に変えていくこともできるのです。
また、平行四辺形の証明で学ぶ論理的思考力は、高校入試だけでなく、今後の数学の学習においても非常に重要な土台となります。
そこで今回は、中学2年生の数学「平行四辺形の証明」について、基本的な性質から証明のポイント、そして苦手を克服する勉強法まで詳しく解説していきます。
平行四辺形の証明が苦手な中学生や、お子様の数学学習にお悩みの保護者様は、ぜひ最後までご覧ください。
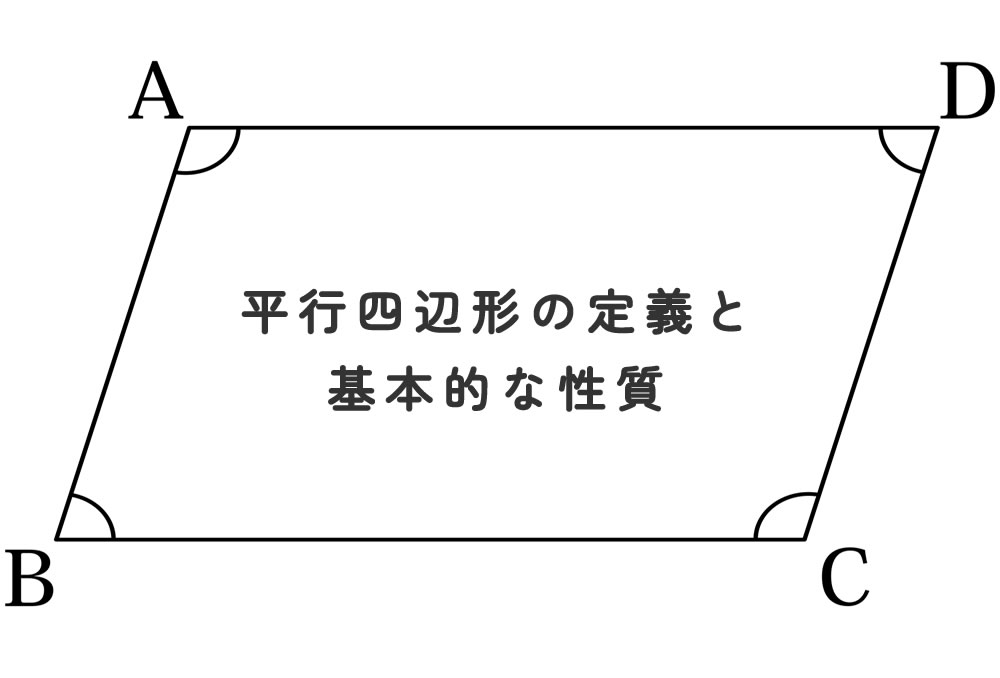
平行四辺形の定義と基本的な性質
「平行四辺形の証明」を解けるようになるためには、まず平行四辺形の定義と基本的な性質をしっかりと理解しておく必要があります。
定義や性質を正しく理解できていないと、証明問題を解く際に、どの条件を使えばよいのかわからなくなってしまいますので、「そもそも平行四辺形とは?」という基本的な定義を押さえておきましょう。
平行四辺形とは?平行四辺形の定義
平行四辺形とは、「2組の向かい合う辺がそれぞれ平行である四角形」のことです。
この定義が平行四辺形の最も基本的な条件となります。
そのため、「2組の向かい合う辺がそれぞれ平行な四角形」であれば、それは平行四辺形といえるのです。
証明問題では、この定義と応用を使って「ある四角形が平行四辺形である」ことを示していきます。
平行四辺形の基本的な性質
平行四辺形には、定義から導かれる重要な性質がいくつかあります。
まずは、「2組の向かい合う辺がそれぞれ平行である四角形にはどのような性質があるのか」、ということを考えてみます。
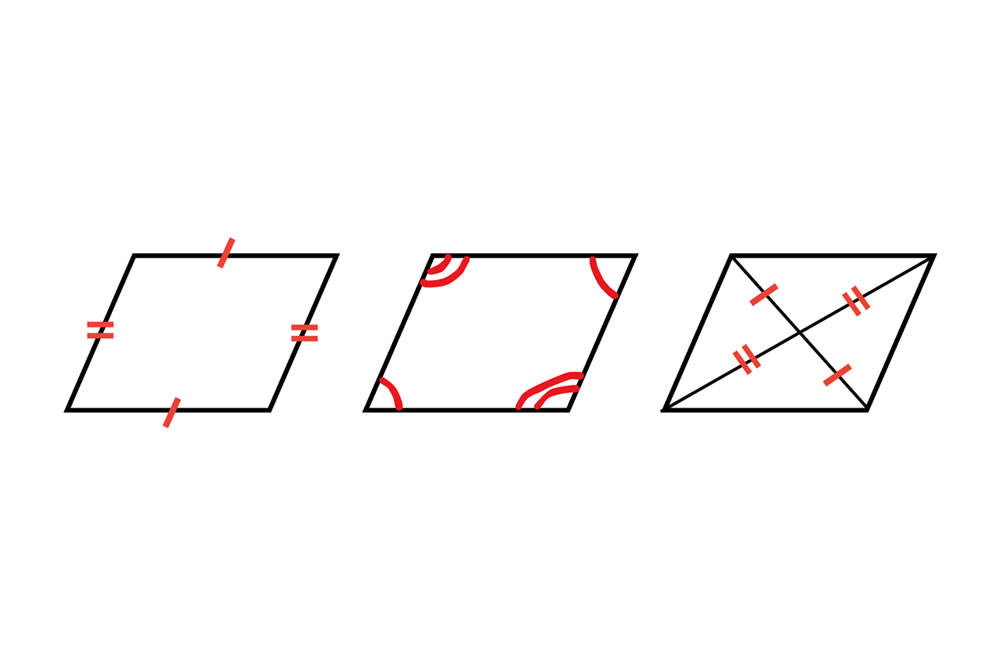
- ・2組の向かい合う辺がそれぞれ等しい
- ・2組の向かい合う角がそれぞれ等しい
- ・対角線がそれぞれの中点で交わる
実際に平行四辺形を描いてみるとわかるのですが、「2組の向かい合う辺がそれぞれ平行である四角形」を描くと、自然と「2組の向かい合う角がそれぞれ等しい」になるはずです。
これらの性質は、平行四辺形の証明問題において頻繁に使用されます。
また、これらの性質を使って、三角形の合同を証明したり、辺の長さや角度を求めたりすることもできますので、非常に重要な性質といえます。
平行四辺形になるための条件
では、ここまで学んだ、平行四辺形の定義や性質を使って、実際に「平行四辺形になるための条件」を確認していきましょう。
平行四辺形の証明問題では、「ある四角形が平行四辺形である」ことを証明する問題が非常によく出題されます。
そのためには、「どのような条件を満たせば平行四辺形といえるのか」を正確に理解しておく必要があります。
平行四辺形になる5つの条件
平行四辺形になるための条件は、定義(2組の向かい合う辺がそれぞれ平行である)を含めて、全部で5つあります。
まずは「5つの条件」をしっかりと理解しましょう。
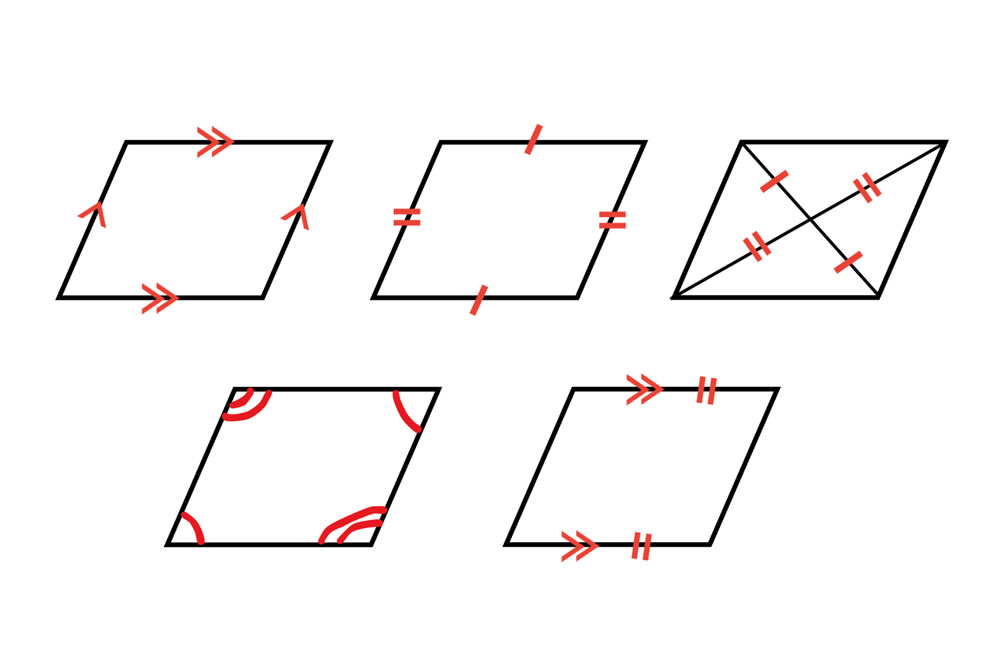
- ・2組の向かい合う辺がそれぞれ平行である
- ・2組の向かい合う辺がそれぞれ等しい
- ・2組の向かい合う角がそれぞれ等しい
- ・対角線がそれぞれの中点で交わる
- ・1組の向かい合う辺が平行で、かつ等しい
証明問題では、これら5つの条件のうち、どれか1つを示すことができれば、その四角形が平行四辺形であることを証明できます。
証明問題を解くためには、問題の図形や与えられた条件によって、「どの条件を使うのが最も適切か」を判断する力が必要になります。
平行四辺形の証明を得意にするテクニック
平行四辺形の証明問題を解く際には、いくつかの基本的な手法やテクニックを理解しておくことが大切です。
これらの手法を組み合わせることで、様々な証明問題に対応することができます。
テクニックさえ知っておけば、証明問題は解きやすく、自分の得意分野にすることも可能です。
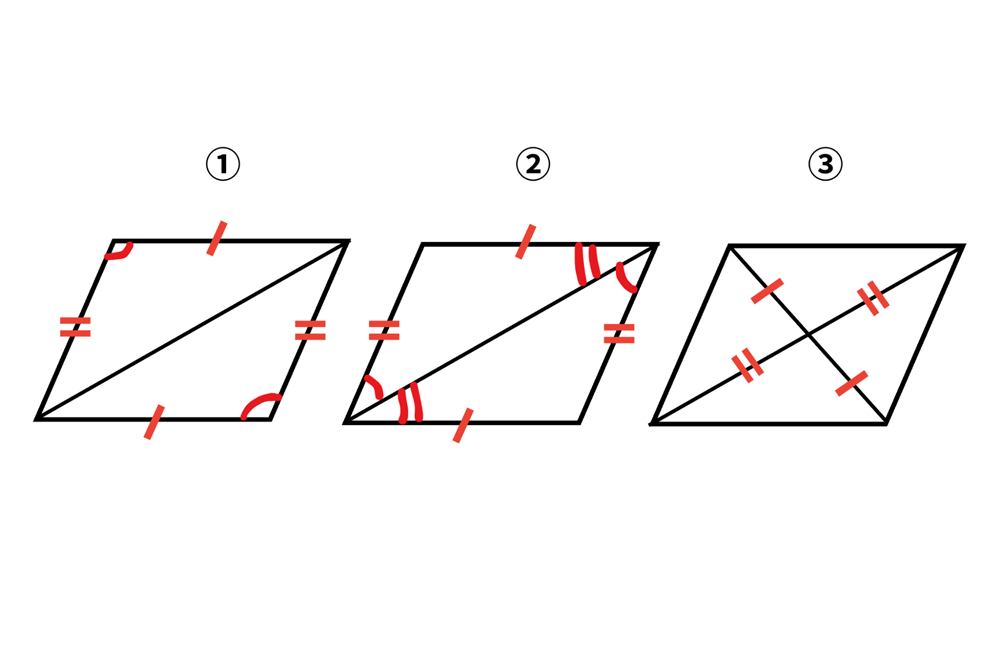
テクニック① 三角形の合同を利用する
平行四辺形の証明では、「三角形の合同」を利用する手法が非常によく使われます。
平行四辺形を対角線で2つの三角形に分割し、それらが合同であることを示すことで、向かい合う辺が等しいことや、向かい合う角が等しいことを証明できます。
三角形の合同条件(3辺が等しい、2辺とその間の角が等しい、1辺とその両端の角が等しい)をしっかりと理解し、使いこなせるようにしておくことが重要です。
テクニック② 錯角や同位角を利用する
平行線と角の関係(錯角、同位角)を利用することも、平行四辺形の証明では欠かせません。
「錯角が等しいならば2直線は平行である」、「同位角が等しいならば2直線は平行である」という性質を使って、辺が平行であることを示すことができます。
逆に、平行であることがわかっている場合には、錯角や同位角が等しいことを利用して、角度の関係を導くこともできます。
テクニック③ 対角線の性質を利用する
平行四辺形の対角線は、それぞれの中点で交わるという性質があります。
この性質を利用して、線分の長さが等しいことを示したり、三角形の合同を証明したりすることができます。
また、逆に対角線がそれぞれの中点で交わることを示すことで、その四角形が平行四辺形であることを証明することも可能です。
平行四辺形の証明が苦手な理由と克服方法
平行四辺形の証明に苦手意識を持つ生徒には、生徒それぞれが持つ「苦手な理由」があります。
「なぜ平行四辺形の証明が苦手なのか」という、「苦手な理由」を明確にして、それぞれの生徒にあった対策を行うことで、証明問題を確実に解けるようになります。
苦手科目を得意科目に変えるためには、生徒一人ひとりの苦手にあった対策を行うことが重要です。
ここでは、証明問題が苦手な生徒が抱えている、「よくある苦手な理由」をご紹介します。
図形の性質を覚えられていない
平行四辺形の証明問題が苦手な理由の多くは、平行四辺形の基本的な性質や条件を正確に覚えられていないことです。
「向かい合う辺が等しい」のか「向かい合う角が等しい」のか、定義と性質が混同してしまうという生徒も少なくありません。
まずは、平行四辺形の定義と5つの条件、基本的な性質を、何度も繰り返して確実に覚える必要があります。
ただ言葉として暗記するのではなく、実際に図を描きながら、それぞれの性質を確認していくことで、理解が深まります。
証明の書き方がわからない
証明問題では、論理的な順序で、わかりやすく説明(証明)を書く必要があります。
「何をどの順番で書けばいいのかわからない」という生徒も多いです。
証明の書き方には一定のパターンがありますので、教科書や問題集の模範解答を何度も読み、証明の流れや書き方を身につけることが大切です。
最初は模範解答を見ながら書き写すだけでも、証明の書き方に慣れていくことができます。
何度も真似して書き写しているうちに、自然と証明問題が得意になるという生徒も少なくありません。
どの性質を使えばいいか判断できない
問題によって、「どの条件や性質を使って証明すればよいのか」は異なります。
「問題を見ても、何から手をつければいいのかわからない」という状態になってしまう生徒の場合、「どの条件を使うか判断する」というトレーニングをすることがおすすめです。
まずは問題文をしっかりと読み、与えられている条件を図に書き込んでみましょう。
そして、何を証明すればよいのかを明確にし、そのために必要な条件は何かを逆算して考える練習を繰り返すことで、判断力が身についていきます。
代々木個別指導学院で「平行四辺形の証明」の苦手を克服!
平行四辺形の証明が苦手な中学生は、「代々木個別指導学院」での学習がおすすめです。
代々木個別指導学院であれば、生徒一人ひとりにジャストフィットした学習が可能ですので、確実に苦手を克服することができます。
「なぜ、代々木個別指導学院であれば苦手を克服できるのか?」という理由を含め、代々木個別指導学院の特徴やメリットをご紹介します。
キミ専用カリキュラムで効率的に学習
代々木個別指導学院では、生徒一人ひとりに合わせた「キミ専用カリキュラム」を作成します。
平行四辺形の証明が苦手な生徒には、基礎から応用まで段階的に学習できるカリキュラムを作成し、定期テストや高校入試に向けて、計画的に力をつけていくことができます。
また、学習の進捗に応じてカリキュラムを柔軟に調整できるため、常に最適な学習を進めることが可能です。
基礎から丁寧に理解できる
代々木個別指導学院のキミ専用カリキュラムであれば、生徒一人ひとりの理解度や進捗状況に合わせて、基礎からじっくりと指導を行います。
平行四辺形の定義や性質があいまいな生徒には、まずはそこから丁寧に説明し、確実に理解できるまでサポートします。
また、証明問題の解き方や書き方についても、一つひとつのステップを丁寧に指導しますので、「わかったつもり」ではなく、「確実にできる」、「自分一人でも解ける」というレベルまで到達することができます。
総合学習アドバイザーによる学習サポート
代々木個別指導学院には、学習指導の専門家である「総合学習アドバイザー」が在籍しています。
総合学習アドバイザーは、生徒の学習状況を総合的に管理し、最適な学習プランを作成します。
平行四辺形の証明だけでなく、数学全体の学習方法や、他の教科とのバランスなども考慮しながら、生徒の成績向上をトータルでサポートします。
平行四辺形の証明を得意単元にして、数学全体が得意科目になるような指導を実施していきます。
まずは無料体験授業で代々木個別指導学院を体感してください
平行四辺形をはじめとした証明問題が苦手な中学生や、数学を得意科目にしたい生徒は、まず代々木個別指導学院の無料体験授業にご参加ください。
無料で実際の授業を体験いただくことができますので、代々木個別指導学院の指導方法や雰囲気を実感していただけます。
また、無料体験授業では、生徒の現在の学力を診断させていただき、苦手克服のための具体的なアドバイスもさせていただきます。
代々木個別指導学院では、生徒一人ひとりに合わせたオーダーメイドの指導により、平行四辺形をはじめとする証明問題など、生徒の苦手を確実に克服し、成績向上を実現いたします。
様々な証明問題でつまずいている生徒や、お子様の学習にお悩みの保護者様は、ぜひお気軽に代々木個別指導学院までご相談ください。